Transportes eficiente precisam de informação

O problema dos transportes coletivos começa pela falta de informação.

Apesar de os autocarros serem tecnologicamente eficientes de transporte de passageiros (i.e, barata),
   Amortização do autocarro -> 0,20€/km (fixo)
   Combustível -> 0,45€/km (variável)
   Manutenção e seguro -> 0,15€/km (meio fixo)
   Motorista -> 0,70€/km(fixo)
 Total -> 1,50€/km, cerca de 0,03€/km por passageiro (com 50 passageiro),
porque a procura é muito variável ao longo do dia, tornam-se ineficientes porque andam quase sempre vazios, com ocupação média inferior a 15%.
De facto, estando o sistema de transporte dimensionado para os períodos de "hora de ponta" (entre as 6h30 e as 9h30 e entre as 17h30 e as 20h30) e como os custos fixos (os motoristas e os autocarros) pesam 2/3 no custo total, a decisão de manter os autocarros a circular vazios não é de todo irracional mas leva a que o sistema se torne globalmente caro e que dê prejuízo. 

As empresas de transportes ainda vivem na idade da pedra!

No sentido de que são geridos sem informação quanto ao que pretendem os clientes.
Hoje, na idade da informação, o mais natural seria que fosse recolhida informação junto de cada cliente para que o desenho das "carreiras" pudesse ser otimizado.
Por exemplo, para os passageiros têm assinatura mensal e fazem viagens com regularidade, deveria ser pedida informação ao cliente usando uma aplicação de telemóvel ou uma página da Internet (ver, Fig. 1).

Fig. 1 - Informação fornecida por um utilizador frequente (dados introduzidos a vermelho).

1 - Para facilitar a identificação das paragens de autocarro, usar-se um par de números que representa a distância em dezenas de metros em relação a um ponto de referência.  Por exemplo,  a paragem 135/216 fica 1350m a Norte e 2160m a Ocidente do ponto de referência e entre a paragem 135/216 e 535/254 distam 4020 m em "voo de pássaro".
2 - O preço a pagar seria em função da distância percorrida, por exemplo, 0,05€ + 4,02km*0,15€/km = 0,653€.
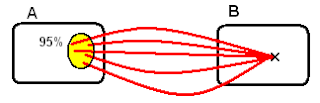
3 - No exemplo da Fig. 1, o sistema iria calcular a que hora o passageiro teria que estar na paragem 135/216 para poder chegar ao destino na hora pretendida, 8h00, com 95% de probabilidade.
4 - O sistema comunicaria (por SMS) ao JSSANTOS a que horas deveria estar na paragem de autocarro 135/216.
5 - Para incentivar o fornecimento de informação, haveria um desconto de 10% no preço da viagem.
6 - Poderiam acabar as assinaturas mensais e, em alternativa, haver um desconto para os clientes frequentes. Por exemplo, um desconto em percentagem correspondente aos quilómetros percorridos durante a semana com um máximo de 50%.
Supondo que JSSANTOS retorna à noite da viagem da Fig. 1  e que não faz mais viagens (um total de 40,2km/semana),  iria pagar  (10*0,653€)*(1-10%)*(1-40,2%) = 3,514€/semana.
Se também voltasse a casa à hora do almoço, pagaria = (20*0,653)*(1-10%)*(1-50%) = 5,877€/semana
Este valor seria debitado na conta do cliente.


A gestão dos veículos.
Agora que a maioria dos clientes já introduziram a informação no sistema (motivado pelos descontos), as carreiras já podem ser desenhadas de forma a minimizar uma função objetivo onde estão incluídos os custos do autocarro, do motoristas e ainda os custos do cliente.

É que o custo da viagem para o cliente tem várias parcelas.

O preço pago pelo bilhete é uma parcela importante do custo incorrido pelo passageiro mas há outras parcelas.

       Parcela 1 --> Preço do bilhete

       Parcela 2 --> Distância percorrida a pé

       Parcela 3 --> Número de transbordos (mudanças de veículo)

       Parcela 4 --> Tempo da viagem

E que fazer aos passageiros eventuais?
Usariam a aplicação de telemóvel ou a Internet para dizer que queriam fazer a viagem. Em último caso, haveria um smartscreen nas paragens dos autocarros para que o cliente introduzisse o destino pretendido (ver, Fig. 2).

Fig. 2 - O cliente eventual carrega num botão e introduz o destino pretendido.

Os veículos deveriam ser mais pequenos.
Os STCP tem 480 autocarros com uma média na ordem dos 100 lugares. Nas horas de ponta é eficiente usar um autocarro com 100 lugares mas, nas restantes horas, não se justificam que circulem com 3 ou 4 passageiros. Se, em alternativa, a frota fosse formada por 3500 carrinhas de 15 lugares, por exemplo,  a Toyota Commuter Hiace (existem outras marcas), haveria possibilidade de fazer carreiras muito mais personalizadas (com a informação existente no sistema) e, nas horas mortas, manter a qualidade do serviço sem manter autocarros enormes em circulação.

Fig. 3 - A Toyota Hiace Commuter é um ligeiro com 14 + 1 lugares sentados (ver vídeo)

O problema é o custo do motorista.
O veículo e combustível fica competitivo
    Amortização do autocarro -> 0,07€/km (fixo)
    Combustível -> 0,15€/km (variável)
    Manutenção e seguro -> 0,05€/km (meio fixo)
 Total -> 0,17€/km, cerca de 0,02€/km por passageiro (com 14 passageiro), mais baixo que o autocarro.
Mas, juntando o custo do motorista, 0,70€/km, o custo dispara para 0,07€/km por passageiro.

Vou imaginar um sistema de transportes coletivos sem motoristas.
No futuro, espero eu que não muito distante, os veículos vão ter capacidade de se auto-conduzirem segundo um plano pré definido.
Com os dados introduzidos no sistema pelo clientes, o sistema vai distribuir os passageiros pelas 35000 carrinhas desenhando trajectórias que minimizem não só os quilómetros globalmente percorridos pelos veículos como também os quilómetros percorridos a pé pelos passageiros, o número de transbordos necessários e o tempo da viagem.
Quando um passageiro eventual carregar no botão a chamar um transporte, o sistema re-calcula todas as trajetórias e escolhe a que induz um menor incremento na função objetivo.

Fig. 4 - Sonho com o dia em que possa dormir enquanto conduzo.

Poderá haver várias empresas no mercado (em concorrência).
Eu sou contra os monopólios. Assim, as carrinhas serão de várias empresas, por exemplo, 50 empresas, as maiores com 100 carrinhas e as menores com 5 carrinhas. As empresas competem pelos clientes. Por exemplo, depois de o cliente submeter a informação da Fig. 1, terá a possibilidade de escolher a proposta que lhe der mais vantagens.
O sistema de gestão dos trajectos também tanto pode ser como o SIBS, uma associação entre as empresas no mercado, ou também haver vários sistemas em concorrência.

E enquanto não houver carros auto-conduzidos?
Antes de haver carros auto-conduzidos, terá que haver comunicação entre os automóveis conduzidos por humanos. Por exemplo, quando o carro da frente travar, comunicar com o nosso sistema de travagem ou, quando quemos entrar na autoestrada, dizemos aos outros carros para nos darem um espaçozinho.
Como isso não existe e ninguém fala no desenvolvimento dos protocolos para que possa existir, provavelmente, os automóveis auto-conduzidos vão cair na classe da clonagem: há 20 anos quando nasceu a Ovelha Dolly, era a grande rotura tecnologia que iria revolucionar tudo e todos hoje já ninguém fala disso.
Não quero crer que, começando pessoas a dizer que é contra a moral cristã haver carros auto-conduzidos ou que põe em causa os empregos dos taxistas, motoristas e que leva à falência a UBER, essa tecnologia entre para o museu como "coisas que iam ser muito importantes mas que nunca chegaram a sê-lo."


Os veículos terão que ser conduzidos por um dos passageiros.

Não podemos, com a nossa classe B da carta europeia, conduzir um veículos ligeiros (Peso Bruto até 3500kg) com mais de 9 passageiros. Mas isto apenas é verdade na Europa Continental pois na Englaterra, estranahmente, já podemos.
Então, o primeiro passo é uma pequena alteração legislativa ao Código da Estrada que permita aos portadores de carta classe B conduzir veículos ligeiros com 15 passageiros mesmo que se limite a velocidade máxima a 60km/h quando viajarem mais de 9 pessoas.
 

A pessoa disponibiliza-se para conduzir o veículo.
A pessoa quando introduz os dados no sistema (rever, Fig. 1) acrescenta que está disponível para conduzir o veículo, quanto quer receber por cada minuto e o tempo máximo que está disponível, em escalões, por exemplo, 3 (ver, Fig. 5).

Fig. 5 - Aprece um ecrã onde as pessoas licitam tempo de condulção. O sistema escolhe o menor preço  mas paga ao passageiro seleccionado o preço do seguinte (leilão por "second price", ver).

As trajetórias serão diferentes.

Porque agora o sistema terá que optimizar (onde inclui a escolha dos melhores motoristas) garantindo que existe sempre um passageiro disponível para conduzir o veículo.

O valor obtido pelo condutor é creditado na sua conta corrente e usado para pagar viagem suas, transferindo o saldo para outras contas (de familiares ou amigos) ou traduzido em dinheiro. 

Podemos ver na Fig. 5 um exemplo simples de uma viagem para 3 pessoas. A viagem começa em A (onde o veículo estava estacionado) e acaba em D (onde o veículo fica estacionado) ficando garantido que todas as pessoas são transportadas sem necessidade de um motorista externo (provavelmente, não é este o trajecto ótimo).

Fig. 6 - Há 3 pessoas a transportar (P1 = A->B; P2 = C->D e P3 = E->F). A pessoa 1 conduz entre A e C e a pessoa 2 (porque é a mais barata) conduz entre C e D.

Fig. 7 - Vamos rápido que a furgonete já está à nossa espera.

E se houver um acidente?
O prejuizo tem que ficar com a empresa não podendo o risco ser transmitido ao condutor pois, nesse caso, deixará de haver condutores disponíveis.

Em Lisboa há uma empresa de partilha de carros (é um "aluguer sem condutor" ao minuto) mas já é a terceira (as duas anteriores falharam)  e não está a arrancar do chão porque transmite para o condutor um exagero de riscos.

Quando o condutor A entra no veículo tem que o observar bem e tomar conta de todas as falhas. Depois, faz o trajeto e estaciona o carro num sítio qualquer. Mesmo que não tenha tido qualquer toque, primeiro, pode ter observado mal (e haver algum dano), depois, se alguma coisa acontecer enquanto o carro está estacionado (por exemplo, vandalismo) e pode estar estacionado dias sem aparecer novo condutor, é o condutor A que tem que pagar os danos que entretanto aconteça, pois ninguém verifica o estado do carro no momento em que é entregue.

Podem achar que é um elevado risco meter o nosso carro na mão de um desconhecido mas tem que se usar a estatística: se algúem estragar o carro, vai para a jarra (muito dificilmente tornará a conduzir).

Finalmente, eu acho o Trump um bom candidato.

Há um ano quando os refugiados estavam a começar a dar às costas da Grécia tínhamos muitos políticos a dizem "deixem vir os refugiados até nós". Passado menos de um ano, as fronteiras estão quase todas fechadas.

Não penso haver qualquer diferença entre dizer "Vou contruir um muro para parar a imigração ilegal" e fazer um muro e dizer "Esse homem é o Satã, temos é que construir pontes" e fazer um muro.

O Trump diz que faz e faz, os outros dizem que não fazem mas fazem.

Será racista, anti-semita, contra as mulheres? 

É como as outras pessoas.

Eu fui na quarta feira ao centro de saúde fazer um corativo à minha mãe que partiu o cotovelo, seriam uma 17h30, e estavam 4 pessoas à espera para a consulta aberta que começaria às 18h com o Dr. Eurico. No entretanto chegou uma cigana que era a quinta pessoa. Não só foi a primeira a ser atendida, como foi logo às 17h30 (não esperou que o Dr. Eurico chegasse).

 - É para não haver problemas pois estão uns quantos lá fora - disse a menina da secretaria a justificar-se às outras 4 pessoas que ficaram para trás.

As pessoas encolheram os ombros.

É o que os americanos chamam descriminação positiva.

Fig. 8 - Na França, com um presidente esquerdista, todo humanista, que diz ser muito amigos dos refugiados, as barracas são para demolir e o povinho que se desenrasque, que fuja para a Bélgica, que vá para o diabo que as carregue.

Read more »

A Estatística, as Sondagens e o erro de previsão

Quando apresentei as "minhas" previsões para as presidenciais (ver) ...

o Abel Lisboa veio dizer "fico sempre preocupado quando vejo um docente da casa (...) a dizer que com 95% de prob. o parâmetro populacional (repito, é uma constante e não tem prob. associadas) está dentro do IC" . A palavra "casa" dá força à conjectura de que esta dúvida foi colocada por um  meu colega de trabalho, talvez.
Sendo assim, sinto a obrigação reforçada de escrever algo mais detalhado sobre este problema pois, a ser verdade o que o Abel Lisboa diz, as sondagens não têm fundamento na Ciência!


As pessoas confundem conceitos.
E, uma vez aprisionadas nessa confusão, não vão aos fundamentos, único local onde podem encontrar a forma de se libertarem desse enredo.
Neste poste vou aos fundamentos da Estatística para explicar como, a partir de uma sondagem (com a qual calculamos proporções) é científico construir um intervalo de confiança sobre os resultados eleitorais (para as proporções na população, que desconhecemos).

A Matemática nunca pode dizer "agora não que estou com dores de cabeça".
A matemática é instrumental  na procura que a Humanidade faz no sentido de compreender o Mundo. Então, tal como a linguagem não pode ser um entrave à comunicação, a matemática nunca pode ser um entrave nesse caminho de procura do conhecimento.
Sendo a Matemática uma construção da humanidade, em presença de um problema que a Matemática não consegue ajudar a resolver, teremos que a fazer evoluir no sentido de nos poder ajudar.
A Matemática não sendo mais que uma linguagem, evolui com as necessidades da Humanidade.
Quando o homem pousou na Lua, tivemos imediatamente que criar a palavra Alunar e, quando surgiram as máquinas programáveis de fazer contas, apareceu imediatamente a palavra Computador.

O que é a Estatística?

A Estatística apareceu quando a "matemática do determinístico" se mostrou incapaz de resolver problemas com um número grande de elementos livres.

Dentro da Matemática temos a Lógica, dentro da Lógica temos a Teoria dos Conjuntos e dentro da Teoria dos Conjuntos temos a Estatística que tem o seu fundamento nos 3 Axiomas de Kolmogorov:

Sendo que existe o conjunto "A", a medida "P" e os sub-conjuntos genéricos disjuntos "a1" e "a2".

Axioma 1:  P(a) >= 0 (A medida "P" sobre o subconjunto "a" é maior ou igual a zero)

Axioma 2:  P(A) =1 (A medida "P" sobre o conjunto "A" é a unidade)

Axioma 3:  P(a1 U a2) = P(a1) + P(a2) (A medida "P" sobre o subconjunto "a1" unido com o
subconjunto "a2" é dado pela soma da medida  "P" sobre o subconjunto "a1" com a medida "P" sobre o subconjunto "a2")

Em termos de linguagem, chamamos a "A" o Conjunto dos Acontecimentos Possíveis e a "P(a)" a Probabilidade de a concretização cair dentro do subconjunto "a".

Vamos agora à sondagem multinomial.

Multinomial quer dizer que o acontecimento tem várias "coisas" em simultâneo. No caso, traduz que acontecem várias proporções ao mesmo tempo, por exemplo, a votação em 5 partidos mais a abstenção, votos nulos e em branco.
Sendo que pretendo fazer uma sondagem, passo a ter dois conjuntos de acontecimentos possíveis.
Por um lado, tenho o conjunto A com todas as proporções possíveis na população e, por outro lado, tenho o conjunto B como todas as proporções possíveis na sondagem.
Havendo 6 proporções possíveis, os conjuntos A e B são IR5 em que cada dimensão vai de 0% a 100%.
A População é um ponto no conjunto A e a "Amostra de dimensão n" é um Ponto no conjunto B.

 Fig. 1 - Para cada população concreta (a cruz dentro de A) correspondem múltiplas sondagens possíveis (uma diferente função P em B)

Será que a Estatística diz algo sob como deve ser A ou B?
Olhemos para os 3 axiomas de Kolmogorov. Será que está lá alguma diferença entre parâmetros e variáveis? Entre coisas que já aconteceram e desconhecemos e coisas que ainda estão para acontecer?
Será que fala lá em variáveis aleatórias, variáveis determinísticas?
Não, nada disso, são coisas muito genéricas.

O que é uma sondagem?
A população é um ponto no conjunto A.
Para, em termos conceptuais, poder extrair uma sondagem tenho, primeiro, que conhecer as proporções na população. Então, o problema concetual que vou resolver é o seguinte:

Conhecendo  as proporções na População (um ponto em A), pretendo saber as propriedades da Amostra (a função P no conjunto B).


Eu ter informação sobre a população (ponto de A que se concretizou), dá-me informação sobre a função P no conjunto B.
Parece estranho eu saber, à partida, as proporções na população quando, aparentemente, é exactamente isso que pretendo prever usando a sondagem. Mas este conhecimento é apenas conceptual, um faz de conta para podermos avançar, uma espécie de backward induction que em linguagem matemática se diz, "Assumido H0".

Este cálculo é impossível em termos algébricos mas torna-se fácil com o Método de Monte Carlo.

A sondagem.

Vou fazer uma sondagem com n = 1500 votos, 900 votos nos "partidos" porque é a dimensão das sondagens usualmente apresentadas pelas televisões.
Para calcular P vou usar simulação estatística (o Método de Monte Carlo)

1 = Fixo a população (uma extracção aleatória);

2 = Faço uma sondagem Extraindo da população obtida em 1 uma amostra com 1500 votos (aleatória);

3 = Calculo as proporções na amostra obtida em 2.
4 = Repito os passos 2 e 3 muitas vezes para poder calcular o desvio padrão.
(Estes quatro pontos estão no Programa 1)

5 = Para tabelar a relação entre a proporção e o erro, repito os passos entre 1 e 4 muitas vezes. 

Apesar de B ser em IR5, as combinações em IR5 não são determinantes em P. Então, vou condensar os resultados em IR (ver, Fig. 2 e tabela1). Multipliquei o desvio padrão por 1,96 para obter o "erro" para uma probabilidade de 95%.

Fig. 2 - Relação entre a proporção e o "erro" para um intervalo de confiança de 95% (900 votos nos partidos)

	Proporção	Erro (95%)	DesvPad
	55%	3,1%	1,6%
	50%	3,1%	1,6%
	45%	3,1%	1,6%
	40%	3,0%	1,5%
	35%	3,0%	1,5%
	30%	2,8%	1,4%
	25%	2,7%	1,4%
	20%	2,5%	1,3%
	15%	2,2%	1,1%
	10%	1,9%	1,0%
	5%	1,4%	0,7%

Tabela 1 - Erro de amostragem numa sondagem com 900 votos válidos num dos partidos

E se eu tiver mais votos?
O erro cai proporcionalmente à raiz quadrada do número de votos. Supondo que tenho agora uma sondagem com 3500 votos expressos e obtenho para o PSD uma proporção de 35%, então, o "erro" a 95% passará a ser (3,0%)* (900/3500)^0,5 = +-1,5%.

Se na população o PSD tiver 35%, na sondagem que vou fazer, o PSD terá uma proporção entre 33,5% e 36,5%, com 95% de confiança

E se tiver mais abstenção?
O erro padrão é apenas dependente do número de votos expressos nos partidos (não interessa a taxa de abstenção).

Mas o que eu quero saber é outra coisa!

Não me interessa saber as propriedades da sondagem (que ainda não fiz) depois de saber a proporção na população mas sim o contrário, quero saber a proporção na população (que não conheço) depois de saber a proporção na sondagem (que já realizei). Então, o problema que vou resolver terá que ser outro:


Conhecida  a proporção na Amostra (um ponto em B) pretendo saber as propriedades da população (a função P no conjunto A).

O que eu quero poder dizer é "Como na amostra com 900 votos válidos o PSD obteve uma proporção de 33%, então,  na população, a proporção estará entre 30,0% e 36% com 95% de confiança."

 Fig. 3 - Cada sondagem concreta (a cruz dentro de B) pode ter origem em múltiplas populações possíveis (uma diferente função P em A)

Segundo o Luís Portugal, isso é impossível de fazer.

O argumento é que a proporção na amostra é um número concreto e não uma variável aleatória.
Mas os 3 axiomas de Kolmogorov não dizem nada disso!
Afinal qual é o axioma que é violado ao afirmar que "o parâmetro estará entre x e y?"
1) Verifica-se que a medida P no conjunto A é unitária.
2) Verifica-se que a medida P num subconjunto de A é  maior ou igual a zero.
3) Verifica-se que a medida na reunião de subconjuntos disjuntos de A é a soma das medidas dos subconjuntos.
Então, nenhum axioma é violado!


Vejamos este exemplo.
Sendo, por definição, um automóvel "uma coisa que se move por meios próprios", então, uma scooter é um automóvel! (ver)
Claro que muita gente irá dizer, "um automóvel é um automóvel e uma scooter é uma scooter" mas apenas porque, mais tarde, alguém nos fez a lavagem ao cérebro de que um automóvel tem que ter 4 rodas.
Mas a definição não fala no número de rodas!
Na Estatística passa-se o mesmo. Têm que ser respeitados os 3 axiomas de Kolmogorov e apenas os 3 axiomas de Kolmogorov mas alguém nos impôs restrições descabidas a que, agora, estamos agarrados e não temos liberdade de pensamento para nos libertarmos dessas amarras.

Como vou agora calcular a coisa?
Para usar o MMC tenho sempre que fazer a sondagem "sob H0". Então, vou ter que fazer diferente do que fiz na Fig. 2 / Tabela 1.

1 = Fixo a população (uma extracção aleatória);
2 = Faço uma sondagem extraindo da população obtida em 1 uma amostra com 900 votos (aleatória);
3 = excluído
4 = Repito os passos 1 e 2 muitas vezes obtendo pares de pontos, uma ordenada em A (população) e outra em B (sondagem).
5 = Com os pares obtidos em 4, calculo o desvio padrão da ordenada que pertencem a A com a restrição de a ordenada em B estar no intervalo ]4,5%; 5,5%] (exemplo para calcular o erro da previsão em A quando temos o resultado 5% na Sondagem).
(Ver, programa 2)

Quais são os resultados?

Obtenho exactamente a Tabela 1!

Quer isto dizer que, em termos estatísticos, o fenómeno é simétrico. Assim, existe propriedade comutativa entre os conjuntos A e B:

Tenho um ponto em A e determino a função P em B

     é equivalente em termos estatísticos a

Tenho um ponto em B e determino a função P em A

E o Bootstraping?
Em A-->B uso a população concreta para calcular as propriedades de P em B.
Em B-->A uso a sondagem concreta para calcular as propriedades de P em A.
Apesar de usar em ambos os casos a população (um ponto em A), haver equivalência entre A-->B e B-->A faz com que o bootstraping (que usa a amostra em vez da população) seja uma metodologia válida.

Tenho que me ir deitar que este poste demorou-me muito tempo a escrever

 #Programa 1 com o código em R

#Proporção na população codificada pela ordem Abst, PSD, PS, BE, CDS, CDU
n <-1500 #Tamanho da amostra
populacao<-c(0.40,0.22,0.20,0.07,0.06,0.05) #Proporções na população
c0<- c1 <-0; c2 <-0; c3 <- 0; c4 <- 0; c5<-0 #Inicialização das variáveis onde se guardam as sondagens
for (i in 1:10000) #Fazem-se 10000 sondagens
    {amostra <- sample(1:6, n, prob=populacao, replace=TRUE) #Sondagem
     res <- table(amostra) #Calcula as proporções na amostra
     res <- res/sum(res[2:6])

    #Guarda as proporções

    c1[i] <- res[2]; c2[i] <- res[3]; c3[i] <- res[4]; c4[i] <- res[5]; c5[i] <- res[6]
    }
c(sd(c1),sd(c2),sd(c3),sd(c4),sd(c5)) #Calculo o desvio padrão de cada proporção
[1] 0.015868676 0.015602831 0.010683888 0.009996019 0.009207823

#Programa 2 com o código em R
abst <-0.40
votos.validos <- 900
n <- votos.validos/(1-abst)
media<-0; desvio<-0; s<-0; a <-0; b <-0
# Sorteia populações e faz uma sondagem para cada população
for (i in 1:20000)
 {#Sorteia uma população em B
   cand <- runif(5,min=0.1,max=3)
   cand <- cand/sum(cand)
   populacao<-c(abst,cand*(1-abst))
  #Tira uma sondagem em B sobre a população anteiror
   amostra <- sample(1:6,n, prob=populacao, replace=TRUE)
   resultado <- table(amostra)
  #Guarda os pontos em A e os correspondentes em B
  for (j in (1:5))
    {a[s+j] <-cand[j];
     b[s+j] <- resultado[j+1]/sum(resultado[2:6])
    }
 s<-s+5
 }
resulta_A<-0
resulta_B<-0
for (j in (1:60))
{resulta_A[j] <- sd(a[b>(j-1)/100 & b<=(j+1)/100])
 resulta_B[j] <- sd(b[a>j/100 & a<=(j+1)/100])
}
x<-data.frame(A<-resulta_A,B<-resulta_B)
write.table(x,file="e://saida.txt",sep=";")

Read more »