Quando apresentei as "minhas" previsões para as presidenciais (ver) ...
o Abel Lisboa veio dizer "fico sempre preocupado quando vejo um docente da casa (...) a dizer que com 95% de prob. o parâmetro populacional
(repito, é uma constante e não tem prob. associadas) está dentro do IC" . A palavra "casa" dá força à conjectura de que esta dúvida foi colocada por um meu colega de trabalho, talvez.
Sendo assim, sinto a obrigação reforçada de escrever algo mais detalhado sobre este problema pois, a ser verdade o que o Abel Lisboa diz, as sondagens não têm fundamento na Ciência!
As pessoas confundem conceitos.
E, uma vez aprisionadas nessa confusão, não vão aos fundamentos, único local onde podem encontrar a forma de se libertarem desse enredo.
Neste poste vou aos fundamentos da Estatística para explicar como, a partir de uma sondagem (com a qual calculamos proporções) é científico construir um intervalo de confiança sobre os resultados eleitorais (para as proporções na população, que desconhecemos).
Sendo assim, sinto a obrigação reforçada de escrever algo mais detalhado sobre este problema pois, a ser verdade o que o Abel Lisboa diz, as sondagens não têm fundamento na Ciência!
As pessoas confundem conceitos.
E, uma vez aprisionadas nessa confusão, não vão aos fundamentos, único local onde podem encontrar a forma de se libertarem desse enredo.
Neste poste vou aos fundamentos da Estatística para explicar como, a partir de uma sondagem (com a qual calculamos proporções) é científico construir um intervalo de confiança sobre os resultados eleitorais (para as proporções na população, que desconhecemos).
A Matemática nunca pode dizer "agora não que estou com dores de cabeça".
A matemática é instrumental na procura que a Humanidade faz no sentido de compreender o Mundo. Então, tal como a linguagem não pode ser um entrave à comunicação, a matemática nunca pode ser um entrave nesse caminho de procura do conhecimento.
Sendo a Matemática uma construção da humanidade, em presença de um problema que a Matemática não consegue ajudar a resolver, teremos que a fazer evoluir no sentido de nos poder ajudar.
A Matemática não sendo mais que uma linguagem, evolui com as necessidades da Humanidade.
Quando o homem pousou na Lua, tivemos imediatamente que criar a palavra Alunar e, quando surgiram as máquinas programáveis de fazer contas, apareceu imediatamente a palavra Computador.
O que é a Estatística?
A Estatística apareceu quando a "matemática do determinístico" se
mostrou incapaz de resolver problemas com um número grande de elementos livres.
Dentro da Matemática temos a Lógica, dentro da Lógica temos a Teoria dos Conjuntos e dentro da Teoria dos Conjuntos temos a Estatística que tem o seu fundamento nos 3 Axiomas de Kolmogorov:
Sendo que existe o conjunto "A", a medida "P" e os sub-conjuntos genéricos disjuntos "a1" e "a2".
Dentro da Matemática temos a Lógica, dentro da Lógica temos a Teoria dos Conjuntos e dentro da Teoria dos Conjuntos temos a Estatística que tem o seu fundamento nos 3 Axiomas de Kolmogorov:
Sendo que existe o conjunto "A", a medida "P" e os sub-conjuntos genéricos disjuntos "a1" e "a2".
Axioma 1: P(a) >= 0 (A medida "P" sobre o subconjunto "a" é maior ou igual a zero)
Axioma 2: P(A) =1 (A medida "P" sobre o conjunto "A" é a unidade)
Axioma 3: P(a1 U a2) = P(a1) + P(a2) (A medida "P" sobre o subconjunto "a1" unido com o
subconjunto "a2" é dado pela soma da medida "P" sobre o subconjunto "a1" com a medida "P" sobre o subconjunto "a2")
Em termos de linguagem, chamamos a "A" o Conjunto dos Acontecimentos Possíveis e a "P(a)" a Probabilidade de a concretização cair dentro do subconjunto "a".
Vamos agora à sondagem multinomial.
Multinomial quer dizer que o acontecimento tem várias "coisas" em simultâneo. No caso, traduz que acontecem várias proporções ao mesmo tempo, por exemplo, a votação em 5 partidos mais a abstenção, votos nulos e em branco.
Sendo que pretendo fazer uma sondagem, passo a ter dois conjuntos de acontecimentos possíveis.
Por um lado, tenho o conjunto A com todas as proporções possíveis na população e, por outro lado, tenho o conjunto B como todas as proporções possíveis na sondagem.
Havendo 6 proporções possíveis, os conjuntos A e B são IR5 em que cada dimensão vai de 0% a 100%.
A População é um ponto no conjunto A e a "Amostra de dimensão n" é um Ponto no conjunto B.
Será que a Estatística diz algo sob como deve ser A ou B?
Olhemos para os 3 axiomas de Kolmogorov. Será que está lá alguma diferença entre parâmetros e variáveis? Entre coisas que já aconteceram e desconhecemos e coisas que ainda estão para acontecer?
Será que fala lá em variáveis aleatórias, variáveis determinísticas?
Não, nada disso, são coisas muito genéricas.
Sendo que pretendo fazer uma sondagem, passo a ter dois conjuntos de acontecimentos possíveis.
Por um lado, tenho o conjunto A com todas as proporções possíveis na população e, por outro lado, tenho o conjunto B como todas as proporções possíveis na sondagem.
Havendo 6 proporções possíveis, os conjuntos A e B são IR5 em que cada dimensão vai de 0% a 100%.
A População é um ponto no conjunto A e a "Amostra de dimensão n" é um Ponto no conjunto B.
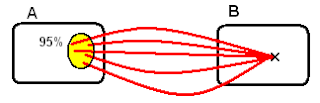
Fig. 1 - Para cada população concreta (a cruz dentro de A) correspondem múltiplas sondagens possíveis (uma diferente função P em B)
Será que a Estatística diz algo sob como deve ser A ou B?
Olhemos para os 3 axiomas de Kolmogorov. Será que está lá alguma diferença entre parâmetros e variáveis? Entre coisas que já aconteceram e desconhecemos e coisas que ainda estão para acontecer?
Será que fala lá em variáveis aleatórias, variáveis determinísticas?
Não, nada disso, são coisas muito genéricas.
O que é uma sondagem?
A população é um ponto no conjunto A.
Para, em termos conceptuais, poder extrair uma sondagem tenho, primeiro, que conhecer as proporções na população. Então, o problema concetual que vou resolver é o seguinte:
Conhecendo as proporções na População (um ponto em A), pretendo saber as propriedades da Amostra (a função P no conjunto B).
Eu ter informação sobre a população (ponto de A que se concretizou), dá-me informação sobre a função P no conjunto B.
Parece estranho eu saber, à partida, as proporções na população quando, aparentemente, é exactamente isso que pretendo prever usando a sondagem. Mas este conhecimento é apenas conceptual, um faz de conta para podermos avançar, uma espécie de backward induction que em linguagem matemática se diz, "Assumido H0".
Este cálculo é impossível em termos algébricos mas torna-se fácil com o Método de Monte Carlo.
A sondagem.
A população é um ponto no conjunto A.
Para, em termos conceptuais, poder extrair uma sondagem tenho, primeiro, que conhecer as proporções na população. Então, o problema concetual que vou resolver é o seguinte:
Conhecendo as proporções na População (um ponto em A), pretendo saber as propriedades da Amostra (a função P no conjunto B).
Eu ter informação sobre a população (ponto de A que se concretizou), dá-me informação sobre a função P no conjunto B.
Parece estranho eu saber, à partida, as proporções na população quando, aparentemente, é exactamente isso que pretendo prever usando a sondagem. Mas este conhecimento é apenas conceptual, um faz de conta para podermos avançar, uma espécie de backward induction que em linguagem matemática se diz, "Assumido H0".
Este cálculo é impossível em termos algébricos mas torna-se fácil com o Método de Monte Carlo.
A sondagem.
Vou fazer uma sondagem com n = 1500 votos, 900 votos nos "partidos" porque é a dimensão das sondagens usualmente apresentadas pelas televisões.
Para calcular P vou usar simulação estatística (o Método de Monte Carlo)
1 = Fixo a população (uma extracção aleatória);
2 = Faço uma sondagem Extraindo da população obtida em 1 uma amostra com 1500 votos (aleatória);
3 = Calculo as proporções na amostra obtida em 2.
4 = Repito os passos 2 e 3 muitas vezes para poder calcular o desvio padrão.
(Estes quatro pontos estão no Programa 1)
5 = Para tabelar a relação entre a proporção e o erro, repito os passos entre 1 e 4 muitas vezes.
Para calcular P vou usar simulação estatística (o Método de Monte Carlo)
1 = Fixo a população (uma extracção aleatória);
2 = Faço uma sondagem Extraindo da população obtida em 1 uma amostra com 1500 votos (aleatória);
3 = Calculo as proporções na amostra obtida em 2.
4 = Repito os passos 2 e 3 muitas vezes para poder calcular o desvio padrão.
(Estes quatro pontos estão no Programa 1)
5 = Para tabelar a relação entre a proporção e o erro, repito os passos entre 1 e 4 muitas vezes.
Apesar de B ser em IR5, as combinações em IR5 não são determinantes em P. Então, vou condensar os resultados em IR (ver, Fig. 2 e tabela1). Multipliquei o desvio padrão por 1,96 para obter o "erro" para uma probabilidade de 95%.
Fig. 2 - Relação entre a proporção e o "erro" para um intervalo de confiança de 95% (900 votos nos partidos)
| Proporção | Erro (95%) | DesvPad | |
| 55% | 3,1% | 1,6% | |
| 50% | 3,1% | 1,6% | |
| 45% | 3,1% | 1,6% | |
| 40% | 3,0% | 1,5% | |
| 35% | 3,0% | 1,5% | |
| 30% | 2,8% | 1,4% | |
| 25% | 2,7% | 1,4% | |
| 20% | 2,5% | 1,3% | |
| 15% | 2,2% | 1,1% | |
| 10% | 1,9% | 1,0% | |
| 5% | 1,4% | 0,7% |
Tabela 1 - Erro de amostragem numa sondagem com 900 votos válidos num dos partidos
E se eu tiver mais votos?
O erro cai proporcionalmente à raiz quadrada do número de votos. Supondo que tenho agora uma sondagem com 3500 votos expressos e obtenho para o PSD uma proporção de 35%, então, o "erro" a 95% passará a ser (3,0%)* (900/3500)^0,5 = +-1,5%.
Se na população o PSD tiver 35%, na sondagem que vou fazer, o PSD terá uma proporção entre 33,5% e 36,5%, com 95% de confiança
E se tiver mais abstenção?
O erro padrão é apenas dependente do número de votos expressos nos partidos (não interessa a taxa de abstenção).
Mas o que eu quero saber é outra coisa!
Não me interessa saber as propriedades da sondagem (que ainda não fiz) depois de saber a proporção na população mas sim o contrário, quero saber a proporção na população (que não conheço) depois de saber a proporção na sondagem (que já realizei). Então, o problema que vou resolver terá que ser outro:
Conhecida a proporção na Amostra (um ponto em B) pretendo saber as propriedades da população (a função P no conjunto A).
Conhecida a proporção na Amostra (um ponto em B) pretendo saber as propriedades da população (a função P no conjunto A).
O que eu quero poder dizer é "Como na amostra com 900 votos válidos o PSD obteve uma proporção de 33%, então, na população, a proporção estará entre 30,0% e 36% com 95% de confiança."
Fig. 3 - Cada sondagem concreta (a cruz dentro de B) pode ter origem em múltiplas populações possíveis (uma diferente função P em A)
Segundo o Luís Portugal, isso é impossível de fazer.
O argumento é que a proporção na amostra é um número concreto e não uma variável aleatória.
Mas os 3 axiomas de Kolmogorov não dizem nada disso!
Afinal qual é o axioma que é violado ao afirmar que "o parâmetro estará entre x e y?"
1) Verifica-se que a medida P no conjunto A é unitária.
2) Verifica-se que a medida P num subconjunto de A é maior ou igual a zero.
3) Verifica-se que a medida na reunião de subconjuntos disjuntos de A é a soma das medidas dos subconjuntos.
Então, nenhum axioma é violado!
Vejamos este exemplo.
Sendo, por definição, um automóvel "uma coisa que se move por meios próprios", então, uma scooter é um automóvel! (ver)
Claro que muita gente irá dizer, "um automóvel é um automóvel e uma scooter é uma scooter" mas apenas porque, mais tarde, alguém nos fez a lavagem ao cérebro de que um automóvel tem que ter 4 rodas.
Mas a definição não fala no número de rodas!
Na Estatística passa-se o mesmo. Têm que ser respeitados os 3 axiomas de Kolmogorov e apenas os 3 axiomas de Kolmogorov mas alguém nos impôs restrições descabidas a que, agora, estamos agarrados e não temos liberdade de pensamento para nos libertarmos dessas amarras.
Como vou agora calcular a coisa?
Para usar o MMC tenho sempre que fazer a sondagem "sob H0". Então, vou ter que fazer diferente do que fiz na Fig. 2 / Tabela 1.
1 = Fixo a população (uma extracção aleatória);
2 = Faço uma sondagem extraindo da população obtida em 1 uma amostra com 900 votos (aleatória);
3 = excluído
4 = Repito os passos 1 e 2 muitas vezes obtendo pares de pontos, uma ordenada em A (população) e outra em B (sondagem).
5 = Com os pares obtidos em 4, calculo o desvio padrão da ordenada que pertencem a A com a restrição de a ordenada em B estar no intervalo ]4,5%; 5,5%] (exemplo para calcular o erro da previsão em A quando temos o resultado 5% na Sondagem).
(Ver, programa 2)
Quais são os resultados?
Mas os 3 axiomas de Kolmogorov não dizem nada disso!
Afinal qual é o axioma que é violado ao afirmar que "o parâmetro estará entre x e y?"
1) Verifica-se que a medida P no conjunto A é unitária.
2) Verifica-se que a medida P num subconjunto de A é maior ou igual a zero.
3) Verifica-se que a medida na reunião de subconjuntos disjuntos de A é a soma das medidas dos subconjuntos.
Então, nenhum axioma é violado!
Vejamos este exemplo.
Sendo, por definição, um automóvel "uma coisa que se move por meios próprios", então, uma scooter é um automóvel! (ver)
Claro que muita gente irá dizer, "um automóvel é um automóvel e uma scooter é uma scooter" mas apenas porque, mais tarde, alguém nos fez a lavagem ao cérebro de que um automóvel tem que ter 4 rodas.
Mas a definição não fala no número de rodas!
Na Estatística passa-se o mesmo. Têm que ser respeitados os 3 axiomas de Kolmogorov e apenas os 3 axiomas de Kolmogorov mas alguém nos impôs restrições descabidas a que, agora, estamos agarrados e não temos liberdade de pensamento para nos libertarmos dessas amarras.
Como vou agora calcular a coisa?
Para usar o MMC tenho sempre que fazer a sondagem "sob H0". Então, vou ter que fazer diferente do que fiz na Fig. 2 / Tabela 1.
1 = Fixo a população (uma extracção aleatória);
2 = Faço uma sondagem extraindo da população obtida em 1 uma amostra com 900 votos (aleatória);
3 = excluído
4 = Repito os passos 1 e 2 muitas vezes obtendo pares de pontos, uma ordenada em A (população) e outra em B (sondagem).
5 = Com os pares obtidos em 4, calculo o desvio padrão da ordenada que pertencem a A com a restrição de a ordenada em B estar no intervalo ]4,5%; 5,5%] (exemplo para calcular o erro da previsão em A quando temos o resultado 5% na Sondagem).
(Ver, programa 2)
Quais são os resultados?
Obtenho exactamente a Tabela 1!
Quer isto dizer que, em termos estatísticos, o fenómeno é simétrico. Assim, existe propriedade comutativa entre os conjuntos A e B:
Tenho um ponto em A e determino a função P em B
é equivalente em termos estatísticos a
Tenho um ponto em B e determino a função P em A
E o Bootstraping?
Em A-->B uso a população concreta para calcular as propriedades de P em B.
Em B-->A uso a sondagem concreta para calcular as propriedades de P em A.
Apesar de usar em ambos os casos a população (um ponto em A), haver equivalência entre A-->B e B-->A faz com que o bootstraping (que usa a amostra em vez da população) seja uma metodologia válida.
#Programa 1 com o código em R
E o Bootstraping?
Em A-->B uso a população concreta para calcular as propriedades de P em B.
Em B-->A uso a sondagem concreta para calcular as propriedades de P em A.
Apesar de usar em ambos os casos a população (um ponto em A), haver equivalência entre A-->B e B-->A faz com que o bootstraping (que usa a amostra em vez da população) seja uma metodologia válida.
Tenho que me ir deitar que este poste demorou-me muito tempo a escrever
#Programa 1 com o código em R
#Proporção na população codificada pela ordem Abst, PSD, PS, BE, CDS, CDU
n <-1500 #Tamanho da amostra
populacao<-c(0.40,0.22,0.20,0.07,0.06,0.05) #Proporções na população
c0<- c1 <-0; c2 <-0; c3 <- 0; c4 <- 0; c5<-0 #Inicialização das variáveis onde se guardam as sondagens
for (i in 1:10000) #Fazem-se 10000 sondagens
{amostra <- sample(1:6, n, prob=populacao, replace=TRUE) #Sondagem
res <- table(amostra) #Calcula as proporções na amostra
res <- res/sum(res[2:6])
n <-1500 #Tamanho da amostra
populacao<-c(0.40,0.22,0.20,0.07,0.06,0.05) #Proporções na população
c0<- c1 <-0; c2 <-0; c3 <- 0; c4 <- 0; c5<-0 #Inicialização das variáveis onde se guardam as sondagens
for (i in 1:10000) #Fazem-se 10000 sondagens
{amostra <- sample(1:6, n, prob=populacao, replace=TRUE) #Sondagem
res <- table(amostra) #Calcula as proporções na amostra
res <- res/sum(res[2:6])
#Guarda as proporções
c1[i] <- res[2]; c2[i] <- res[3]; c3[i] <- res[4]; c4[i] <- res[5]; c5[i] <- res[6]
}
c(sd(c1),sd(c2),sd(c3),sd(c4),sd(c5)) #Calculo o desvio padrão de cada proporção
[1] 0.015868676 0.015602831 0.010683888 0.009996019 0.009207823
}
c(sd(c1),sd(c2),sd(c3),sd(c4),sd(c5)) #Calculo o desvio padrão de cada proporção
[1] 0.015868676 0.015602831 0.010683888 0.009996019 0.009207823
#Programa 2 com o código em R
abst <-0.40
votos.validos <- 900
n <- votos.validos/(1-abst)
media<-0; desvio<-0; s<-0; a <-0; b <-0
# Sorteia populações e faz uma sondagem para cada população
for (i in 1:20000)
{#Sorteia uma população em B
cand <- runif(5,min=0.1,max=3)
cand <- cand/sum(cand)
populacao<-c(abst,cand*(1-abst))
#Tira uma sondagem em B sobre a população anteiror
amostra <- sample(1:6,n, prob=populacao, replace=TRUE)
resultado <- table(amostra)
#Guarda os pontos em A e os correspondentes em B
for (j in (1:5))
{a[s+j] <-cand[j];
b[s+j] <- resultado[j+1]/sum(resultado[2:6])
}
s<-s+5
}
resulta_A<-0
resulta_B<-0
for (j in (1:60))
{resulta_A[j] <- sd(a[b>(j-1)/100 & b<=(j+1)/100])
resulta_B[j] <- sd(b[a>j/100 & a<=(j+1)/100])
}
x<-data.frame(A<-resulta_A,B<-resulta_B)
write.table(x,file="e://saida.txt",sep=";")
 segunda-feira, fevereiro 01, 2016
segunda-feira, fevereiro 01, 2016
















4 comentários:
Qual é a probabilidade de uma obrigação a 3 anos que paga 8% de juros entrar em incumprimento,como se calcula? Preciso da resposta para uma entrevista
Olá Tiago,
PAra calcular a taxa de incumprimento, TInc, temos que saber mais coisas.
1) A taxa de juro sem risco, rsr, por exemplo, 0,200%/ano.
2) O hair-cut, hc, que traduz quantas perdas o incumprimento vai causar, por exemplo, 30%.
Agora, já podemos fazer as contas tornando, em média, o resultado sem risco igual ao resultado com risco (agente neutro ao risco ou que consegue diversificar):
100*(1+rsr)^3 =100*(1+8%)^3*(1-PInc) + 100*(1+8%)^3*(1-hc)*PInc
(1+rsr)^3/(1+8%)^3 =1-PInc + PInc-hc*PInc
(1+rsr)^3/(1+8%)^3 =1
PInc = (1-(1+rsr)^3/(1+8%)^3)/hc
Com os valores considerados em 1) e 2) dará:
PInc = (1-(1+0,2%)^3/(1+8%)^3)/30%
PInc = 67%
Muito obrigado pela reposta. A taxa rsr podemos utilizar as obrigações dos EUA a 3 anos, e uma obrigacao em dólares? Quanto ao hc sendo uma obrigacao empresarial o mais correto nao seria os 100 %?
Tiago,
Se a empresa for em Portugal, o melhor é usar a taxa de juro da dívida pública portuguesa (pois, Portugal evitará a bancarrota cobrando mais impostos às empresas portuguesas).
A perda pode não ser 100%, teria que ser feita uma análise estatística sobre a perda nas obrigações em caso de restruturação/falência de empresas portuguesas. Por exemplo, a Pharol pensa vir a recuperar 15% do dinheiro que meteu em obrigações da Rio Forte, hc = 85%.
Enviar um comentário